Pretraining Large Language Models with NVFP4

https://arxiv.org/pdf/2509.25149v1

Summary

Training methodology

In short, the recommendation for NVFP4 training is:

1. Keep a few sensitive linear layers in higher precision (15% of the network, with the majority of high precision layers at the end of the network).
2. Apply Random Hadamard transforms of size 16×16 to inputs of weight gradient GEMMs.
3. Use two-dimensional (2D) scaling over 16×16 blocks for weights, and one dimensional scaling over 1×16 blocks for activations and gradients.
4. Use stochastic rounding for gradients and round-to-nearest-even for weights and activations.

What’s kept in high precision

• The last layers are kept in high precision
• To ensure numerical stability during training, they retain the original precision (e.g., BF16 or FP32) for
  • embeddings,
  • the output projection head,
  • normalization layers, non-linearities
  • attention components, including softmax and the query-key and attention score-value batched GEMMs.
• The main weights (stored by the optimizer), weight gradients (used for gradient accumulation across microbatches and across data-parallel replicas), and optimizer states are also kept in FP32.
• Tensor parallel reductions are performed in BF16 precision.

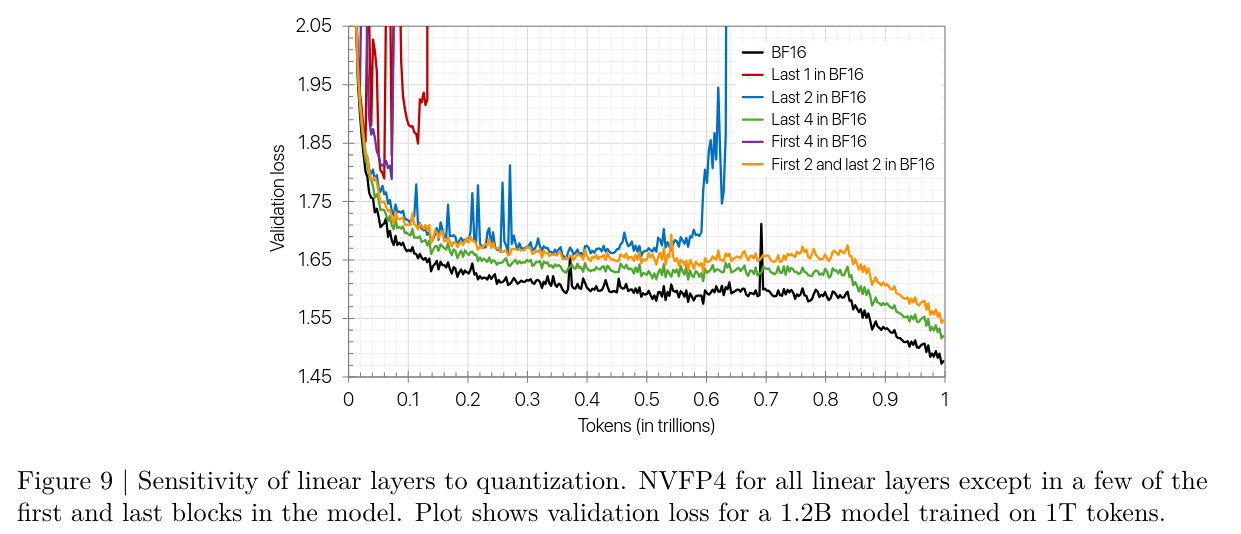
Linear layer sensitivity analysis

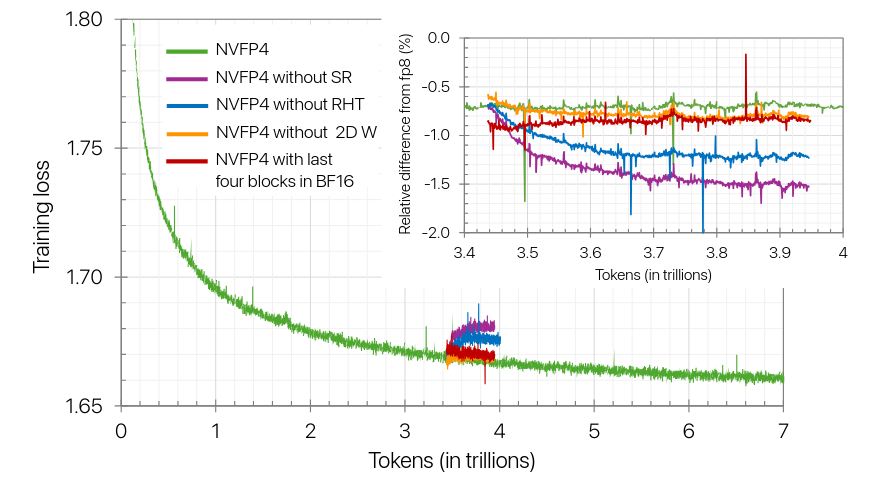
• Although linear layers are typically computed in narrower precisions, we observe that some linear layers are more sensitive to FP4 than others.

• In particular, training diverges when every linear layer is quantized to FP4

• 

• Based on tensor analysis, they observe the last layers tend to have larger quantization errors in the weight gradients (i.e., Wgrad output from its inputs being FP4).

• Quantization error metrics could potentially serve as a mechanism to determine which linear layers should remain in higher precision during training.

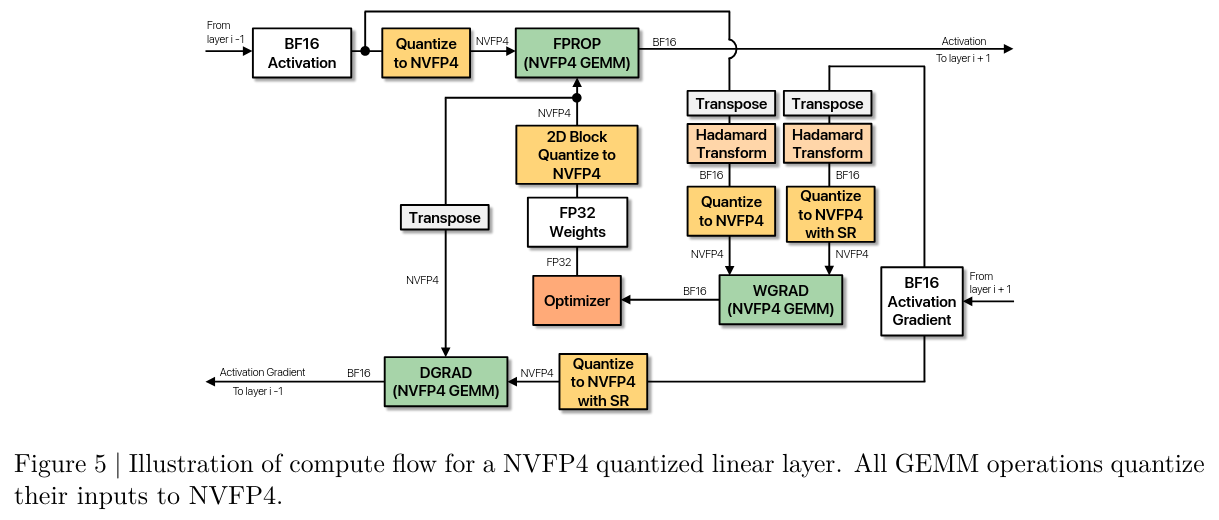
Summary of the NVFP4 quantized linear layer recipe

• GEMM operations consume FP4 tensors as inputs and produce outputs in BF16 or FP32.
• 

Random Hadamard Transforms

What’s that?

• Random Hadamard transforms (RHTs) are useful for smoothing out the spectrum of a matrix and reducing outliers. More details in Using orthogonal matrices for better quantization - The math

• Random Hadamard transforms applies an orthogonal rotation to the tensor being quantized, i.e., $x^{\prime }=q(xH\cdot s)$ where $s$ is the scale factor computed in the rotated space $xH$

• Hadamard matrices are orthogonal, so $C=(AH)(H^{T}B)=AB$

• They perform Hadamard transforms in a tiled approach by multiplying $H$, which has $d\times d$ matrix entries, with an $m\times k$ tensor, where every $d\times d$ elements of the tensor are multiplied by H.

  • The transform involves $(m/d\ast k/d)\ast d^3=mkd$ multiply-adds and $d^2$ reads for the Hadamard matrix.
  • Very easy to implement as a batched matrix mutliply using tensor cores.

• Having some randomness is important, but beyond that using the same RHT for all layers is fine. Can be more important as the model gets bigger though.

When to apply them

• They use RHT to only one GEMM, Wgrad. They apply to both inputs of the GEMM i.e. output-grad and input activations.

  • Assuming $Y=XW$ where $X$ is input activations and $W$ the weights
  • reminder Wgrad $=\frac{\delta L}{\delta W}=\frac{\delta L}{\delta Y}\frac{\delta Y}{\delta W}=X^T(\frac{\delta L}{\delta Y})$

• They only apply to Wgrad, as they found performance to be worse when applying to Fprop or Dgrad ⇒ RHT introduces some amount of noise, which is only beneficial if outlier removal offsets this noise.

Choosing the dimension $d$

• As shown in Using orthogonal matrices for better quantization - The math, for a vector of size $d$, the MSE of the quantization error will tend to multiplied by a factor of $\sqrt{\frac{2\log d}{d}}$
  • For a 4x4 matrix applied on a 4x4 tensor, that’s about $\sqrt{\frac{2\log 16}{16}}=\sqrt{\frac{1}{2}}$
  • For a 16x16 matrix applied on a 16x16 tensor, that’s about $\sqrt{\frac{2\log 2^8}{2^8}}=\sqrt{\frac{2^4}{2^8}}=\frac{1}{4}$
• Need to balance with speed and error reduction
• They ran ablations, and saw that 16x16 was sufficient
  • 
  • Dependent on model scale, larger models may require larger HRT, but this can always swapped during training

2D scaling

• As a reminder, assuming $Y=XW$ where $X$ is input activations and $W$ the weights

  • then Xgrad $=\frac{\delta L}{\delta X}=\frac{\delta L}{\delta Y}\frac{\delta Y}{\delta X}=(\frac{\delta L}{\delta Y})W^T$

• This means that we use $W$ in the forward pass and $W^T$ in the backward pass.

• During training, transform and scaling operations are applied along the dot-product dimension.

• As a result, the same tensor $W$ can have two distinct quantized representations, one during forward and one during backward.

  • Note that this is also the case for $X$, but this seems to be less problematic.
  • The main hypothesis is that $X^T$ only contributes to Wgrad, where as $W^T$ contributes to Xgrad, which will flow through the model layers during backpropagation.

• Block scaling: To mitigate this issue, they propose a 2D block scaling method that ensures consistent quantization in both forward and backward passes for the weights.

  • For weights, elements are grouped and scaled in $16\times 16$ (16 input channels by 16 output channels) like in DeepSeek-v3
  • To implement this in practice, they compute the scale once for the 16x16 block and then replicate it for each of the 1x16 block when being passed to the Tensor Cores.

• Activations and gradients use the standard NVFP4 scaling (i.e., 1 × 16 blocks), since finer-grained scaling improves quantization accuracy.

  • Weights are also more tolerant to the scale granularity because they can adapt to the FP4 values

Stochastic rounding

• During quantization to FP4, deterministic rounding (e.g., round-to-nearest-even) can introduce bias.

• Stochastic rounding rounds a value probabilistically to one of its two nearest representable numbers, with probabilities inversely proportional to their distances.

  • This prevents values from being consistently quantized in the same direction, thereby reducing bias.

• The effect of bias is typically more pronounced in gradient tensors, which can impact training convergence.

• To address this bias, they adopt stochastic rounding during quantization of the output gradient values to FP4.

  • They found it to be essential for the convergence of the 12B model
    • 

• Other tensors in the backward pass do not benefit from stochastic rounding.

• Applying stochastic rounding to the forward pass tensors is detrimental, as it amplifies quantization error relative to nearest rounding