Sharded Matmuls

• https://jax-ml.github.io/scaling-book/sharding/

A unified notation for sharding

We use a variant of named-axis notation to describe how the tensor is sharded in blocks across the devices: we assume the existence of a 2D or 3D grid of devices called the device mesh where each axis has been given mesh axis names e.g. X, Y, and Z. We can then specify how the matrix data is laid out across the device mesh by describing how each named dimension of the array is partitioned across the physical mesh axes. We call this assignment a sharding.

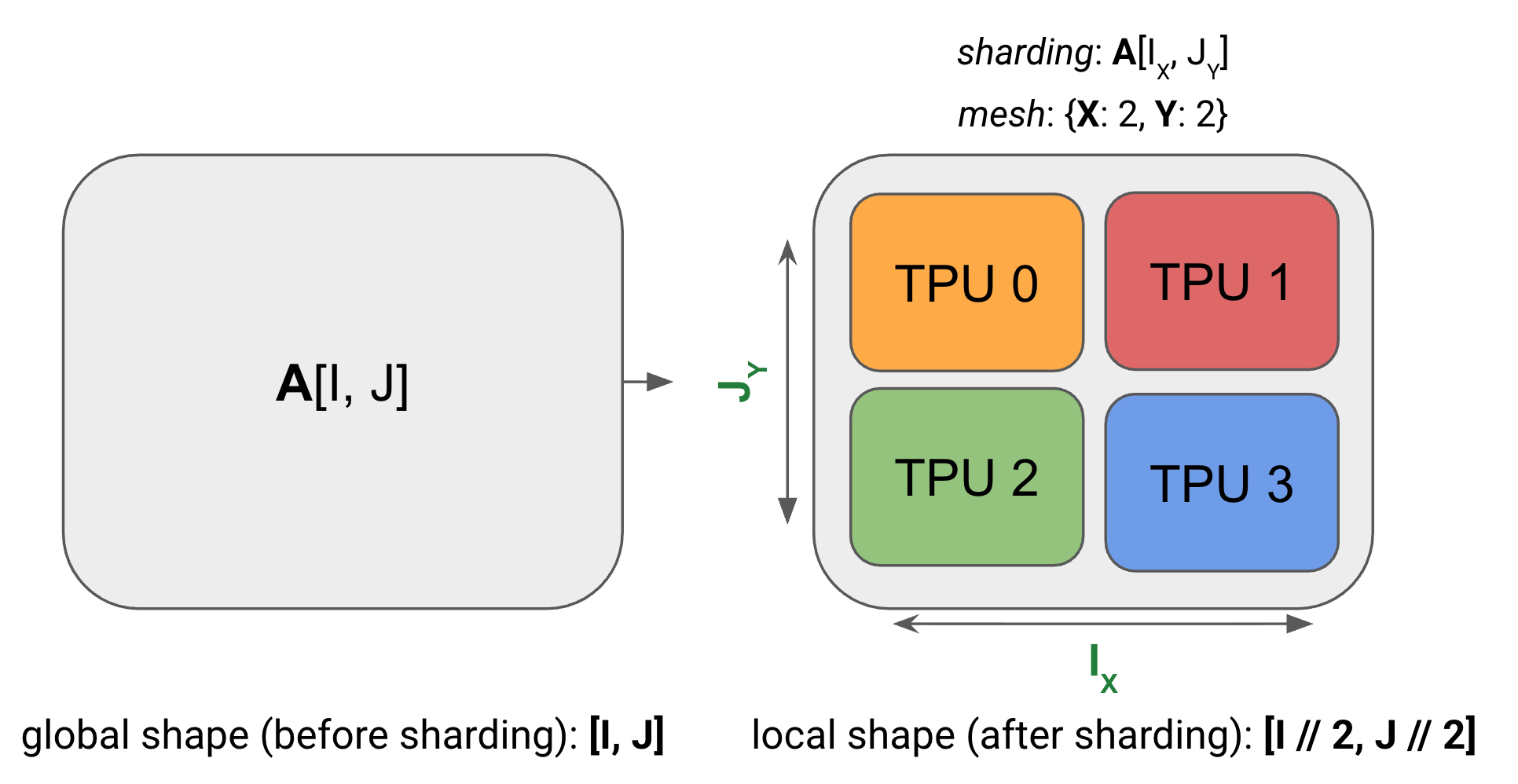
Example (the diagram above): For the above diagram, we have:

• Mesh: the device mesh above Mesh(devices=((0, 1), (2, 3)), axis_names=(‘X', ‘Y')), which tells us we have 4 TPUs in a 2x2 grid, with axis names X and Y .
• Sharding: $A[I_X,J_Y]$ , which tells us to shard the first axis, $I$ , along the mesh axis $X$ , and the second axis, $J$ , along the mesh axis $Y$ . This sharding tells us that each shard holds $1/(\mid X\mid \cdot \mid Y\mid )$ of the array.

Lastly, note that we cannot have multiple named axes sharded along the same mesh dimension. e.g. $A[I_X,J_X]$ is a nonsensical, forbidden sharding. Once a mesh dimension has been used to shard one dimension of an array, it is in a sense “spent”.

Computation with sharded arrays

Case 1: neither multiplicand has a sharded contracting dimension

Lemma: when multiplying sharded matrices, the computation is valid and the output follows the sharding of the inputs unless the contracting dimension is sharded or both matrices are sharded along the same axis.

For example, this works fine \begin{equation*} \mathbf{A}[I_X, J] \cdot \mathbf{B}[J, K_Y] \rightarrow \mathbf{C}[I_X, K_Y] \end{equation*} with no communication whatsoever, and results in a tensor sharded across both the X and Y hardware dimensions.

Case 2: one multiplicand has a sharded contracting dimension

Let’s consider what to do when one input A is sharded along the contracting J dimension and B is fully replicated: $\mathbf{A}[I,J_X]\cdot \mathbf{B}[J,K]\to \mathbf{C}[I,K]$

We cannot simply multiply the local chunks of A and B because we need to sum over the full contracting dimension of A, which is split across the X axis. Typically, we first “AllGather” the shards of A so every device has a full copy, and only then multiply against B:

${\text{AllGather}}_X[I,J_X]\to \mathbf{A}[I,J]$ $\mathbf{A}[I,J]\cdot \mathbf{B}[J,K]\to \mathbf{C}[I,K]$

• When multiply matrices where one of the matrices is sharded along the contracting dimension, we generally AllGather it first so the contraction is no longer sharded, then do a local matmul.

Case 3: both multiplicands have sharded contracting dimensions

The third fundamental case is when both multiplicands are sharded on their contracting dimensions, along the same mesh axis:

$\text{A}[I,J_X]\cdot \text{B}[J_X,K]\to C[I,K]$

• In this case the local sharded block matrix multiplies are at least possible to perform, since they will share the same sets of contracting indices.

• But each product will only represent a partial sum of the full desired product i.e. partial sum of outer products.

  • A matmul can be defined as a sum of rank-1 outer products $A\cdot B={\sum }_{i=1}^K\underset{\in {\mathbb{R}}^{n\times m}}{\underbrace{A_{:,i}\otimes B_{i,:}}}$

• This is so common that we extend our notation to explicitly mark this condition: $\text{A}[I,J_X]{\cdot }_{\text{LOCAL}}\text{B}[J_X,K]\to C[I,K]\{U_X\}$

• The notation $\{U_X\}$ reads “unreduced along X mesh axis” and refers to this status of the operation being “incomplete” in a sense, in that it will only be finished pending a final sum.

• We can perform this summation using a full AllReduce across the X axis to remedy this: \begin{align*} A[I, J_X] \cdot_\text{LOCAL} B[J_X, K] \rightarrow &\ C[I, K] \{ U_X \} \\ \textbf{AllReduce}_X C[I, K] \{ U_X \} \rightarrow &\ C[I, K] \end{align*}

• AllReduce removes partial sums, resulting in each device along the axis having the same fully-summed value.

Case 4: both multiplicands have a non-contracting dimension sharded along the same axis

Each mesh dimension can appear at most once when sharding a tensor. Performing the above rules can sometimes lead to a situation where this rule is violated, such as:

$A[I_X,J]\cdot B[J,K_X]\to C[I_X,K_X]$ This is invalid because a given shard, say i, along dimension X, would have the (i, i)th shard of C, that is, a diagonal entry. There is not enough information among all shards, then, to recover anything but the diagonal entries of the result, so we cannot allow this sharding.

The way to resolve this either to $AllGathe{r}_X$ A or B.

Communication Primitives

AllGather

• An AllGather removes the sharding along an axis and reassembles the shards spread across devices onto each device along that axis.
• Using the notation above, an AllGather removes a subscript from a set of axes, e.g. ${\text{AllGather}}_X(A[I_X,J])\to A[I,J]$

How is it performed?

• To perform a 1-dimensional AllGather around a single GPU axis (a ring), we basically have each GPU pass its shard around a ring until every device has a copy.
• We can either do an AllGather in one direction or both directions
  • If we do one direction, each TPU sends chunks of size $bytes/N$ over $N-1$ hops around the ring. If we do two directions, we send 2 chunks of size $bytes/N$ over $N/2$ hops.

Runtime

• Let’s take the bidirectional AllGather and calculate how long it takes.

• Let be $V$ the number of bytes in the array, and $X$ be the number of shards on the contracting dimension.

• Then from the above diagram, each hop sends $V/\mid X\mid$bytes in each direction, so each hop takes $T_{hop}=\frac{2\cdot V}{X\cdot W_{\text{ici}}}$

• Here, we assume that the GPU $X_i$ sends one chunk and receives one, thus 2 chunks are sent through the bidirectional link. $W_{ici}$ is the bidirectional ICI bandwidth.

• A given GPU will need to send a total of $|X|/2$ hops so that its own shard reaches the other end of the ring

• Thus, the total reduction takes $T_{total}=\frac{2\cdot V\cdot X}{2\cdot X\cdot W_{\text{ici}}}=\frac{V}{W_{\text{ici}}}$

• This doesn’t depend on the sharding $X$!

  • The exact sharding doesn’t matter, the bottleneck is the speed of the slowest link

• TAKEAWAY: when performing an AllGather (or a ReduceScatter or AllReduce) in a throughput-bound regime, the actual communication time depends only on the size of the array and the available bandwidth, not the number of devices over which our array is sharded!

  • The reason why the number of devices is still a problem in practice is because within a node, the weakest link is NVLink, where as going multi-node, the weakest link is InfiniBand

ReduceScatter

• A ReduceScatter sums an unreduced/partially summed array and then scatters (shards) a different logical axis along the same mesh axis $[F]\{U_Y\}\to [F_Y]$
• The signature is:

\begin{align*} \textbf{ReduceScatter}_{Y,J} : A[I_X,J] \{U_Y\} \rightarrow &\ A[I_X, J_Y]\end{align*}

• How does it work?

  • Assume a logical ring $GP{U}_0\to GP{U}_1\to \dots \to GP{U}_N\to GP{U}_0$

  • Each $GP{U}_i$ starts with a tensor $x_i$​, which we’ll assume we will split into N equal-sized chunks:

    • $x_i=[x_{i,0},x_{i,1},\dots ,x_{i,N}]$
    • where $x_{i,j}$ means the j-th chunk of the tensor on $GP{U}_i$

  • Let’s assume the one-directional algorithm for simplicity.

  • Each GPU $i$ will accumulate into its tensor $x_i$ the chunks of other neighbors.

  • There will be $N-1$ rounds, $s=0\dots N-2$ , the steps for $GP{U}_i$

    1. Send chunk index $(i-s)modN$ to your right neighbor.
    2. Receive chunk index $(i-1-s)modN$ from your left neighbor.
    3. Accumulate (sum) the received chunk into your local buffer for that chunk

  • After $N-1$ rounds, each chunk has visited every GPU once and has been fully reduced.

  • Final ownership in the NCCL ring is a +1 rotation

    • Indeed, the final chunk $GP{U}_i$ receives chunk index $i-N+1modN=i+1modN$
    • i.e. $GP{U}_i$ owns chunk $x_{i+1modN}$

  • One more cyclic hop will have each GPU owning the correct chunk

• How long does it take?

  • Same runtime, as an all-gather, each GPU sends chunk of $V/N$ bytes $N$ times (one-directional) or 2 chunks of $V/N$ bytes $N/2$ times (bi-directional)

AllReduce

• An AllReduce takes an array with an unreduced (partially summed) axis and performs the sum by passing those shards around the unreduced axis and accumulating the result.
• The signature is:

${\text{AllReduce}}_{Y}A[I_X,J]\{U_Y\}\to A[I_X,J]$

• This means it simply removes the $\{U_Y\}$ suffix but otherwise leaves the result unchanged. ⇒ an all-reduce doesn’t change the sharding

• AllReduce = reduceScatter + AllGather \begin{align*} \textbf{ReduceScatter}_{Y,J} : A[I_X,J] \{U_Y\} \rightarrow &\ A[I_X, J_Y] \\ \textbf{AllGather}_Y : A[I_X, J_Y] \rightarrow &\ A[I_X, J] \end{align*}

• Thus, its runtime is 2 times the one of AllGather

AllToAll

• Fundamental collective which does not occur naturally when considering sharded matrix multiplies

• The AllToAll collective is a sharded transposition or resharding operation. ${\text{AllToAll}}_{X,J}A[I_X,J]\to A[I,J_X]$

• One example is if you want to shard along sequence length instead of channel-wise, when going from LayerNorm to context-parallel attention

• This arises naturally when considering MoE models.

  • you compute the gating ⇒ now we need to send and receive the corresponding shards for the expert present on the ranks.
  • you move the sharding from sequence to EP

• An AllToAll only has to pass shards part-way around the ring and is thus ¼ the cost of an AllGather