Definition
- Takes:
- An input array [x0,…,xn]
- An associate operator ⊕
- e.g. sum, product, min, max
- Returns:
- An output array [y0,…,yn−1]
- Inclusive scan: yi=x0⊕…⊕xi
- Excluse scan: yi=x0⊕…⊕xi−1
Parallel scan
- Parallel scan requires synchronization across parallel workers
- On GPUs, it’s cheaper to synchronize with threads on the same thread block compared to across blocks.
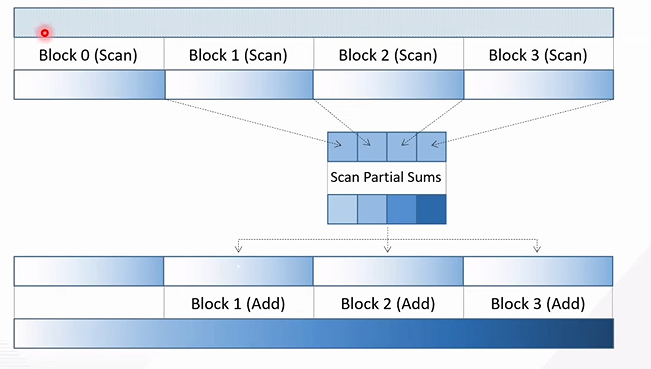
Segmented scan
- Approach: segmented scan
- Every thread block scans a segment
- Scan the segments’ partial sums (parallel across blocks)
- Add each segment’s scanned partial sum last value to the next segment
- This is another scan but with the last value of each segments.
- Diagram
Parallel scan implementation within a single thread block
Kogge-Stone
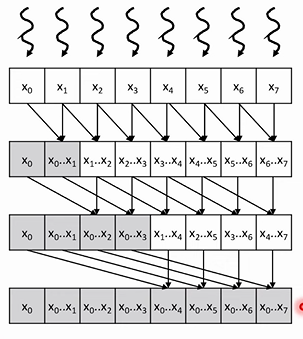
Kogge-Stone example with 8 elements
- We’re looking at parallel (inclusive) scan
- Let’s do ONE parallel reduction tree
- We write in place in the same array
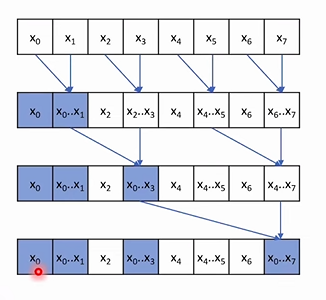
- We get the last element, and some other as byproduct
- Blue values are “already valid” solutions
- SOME VALUE ARE NEVER TOUCHED e.g. x2,x4,x6
- Now, if we overlap and do 4 reduction trees, we get
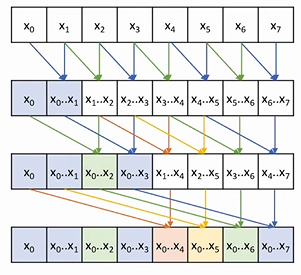
- First iteration: for every element, add the element one step before it
- Second iteration: for every element, add the element two steps before it
- Third iteration: for every element, add the element four steps before it
- We get O(logN) iterations
Kogge-Stone Parallel (Inclusive) Scan
- Use the above algorithm with one thread for each element
Runtime analysis
- A parallel algorithm is work-efficient if it performs the same amount of work as the corresponding sequential algorithm
- Scan work efficiency
- Sequential scan performs N additions
- Kogge-Stone parallel scan performs:
- log(N) steps, N−2step operations per step
- Total: (N−1)+(N−2)+…+(N−N/2)=N∗log(N)−(N−1)==O(N∗log(N)) operations
- Algorithm is not work efficient
- If resources are limited, parallel algorithm will be slow because of low work efficiency
Implementation
Memory optimization
- The input array x is in global memory
- It doesn’t make sense to keep reading and writing to and from global memory
- Load once to a shared memory buffer, and do everything in shared memory
- Write out at the end
Details
- You need to sync the threads between every iteration
- You need to be careful of race conditions
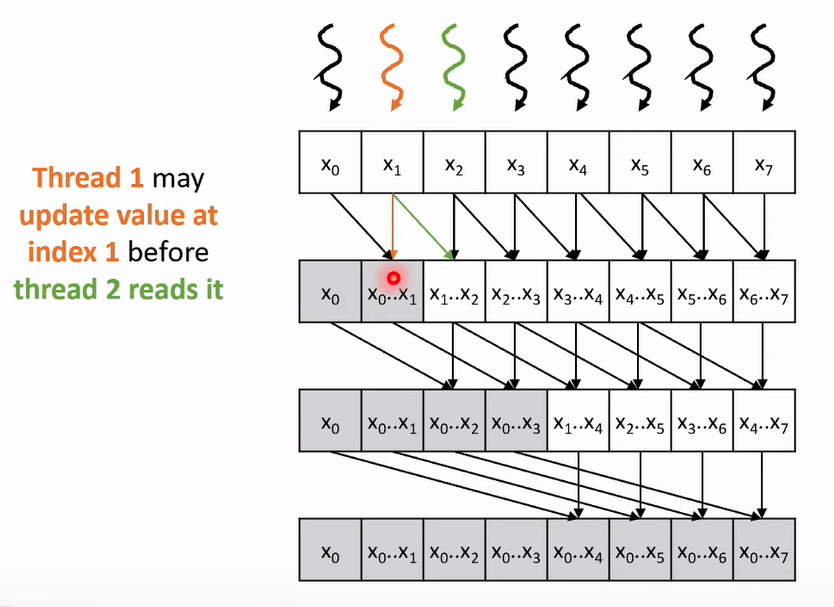
- To fix it, you need to ensure that all threads finish reading, before starting to write
- read →
__syncthreads(); → write
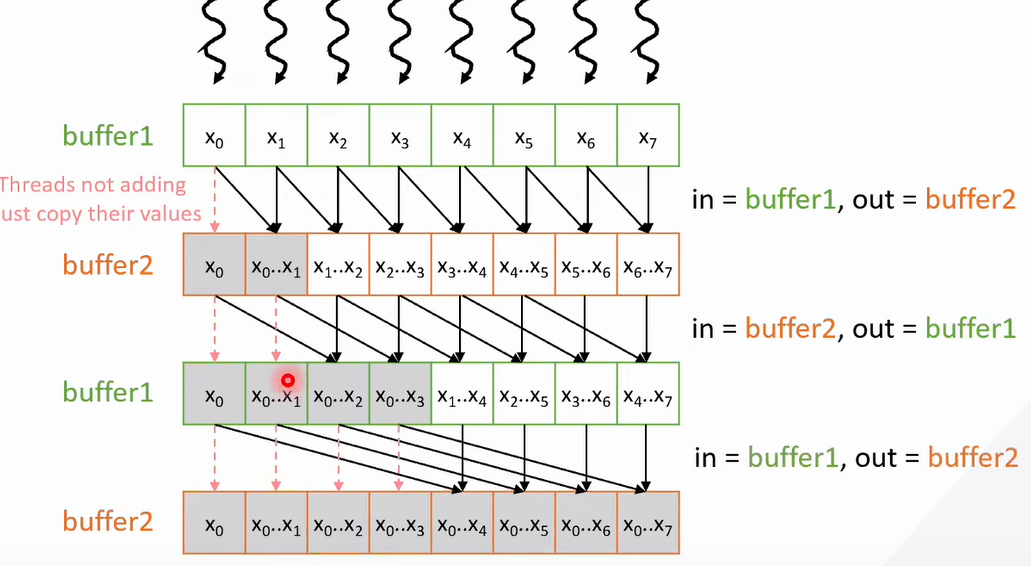
- Better way to do it
- double buffering
- read from buffer1, write to buffer 2
- alternate (read from buffer 2, write in buffer 1)
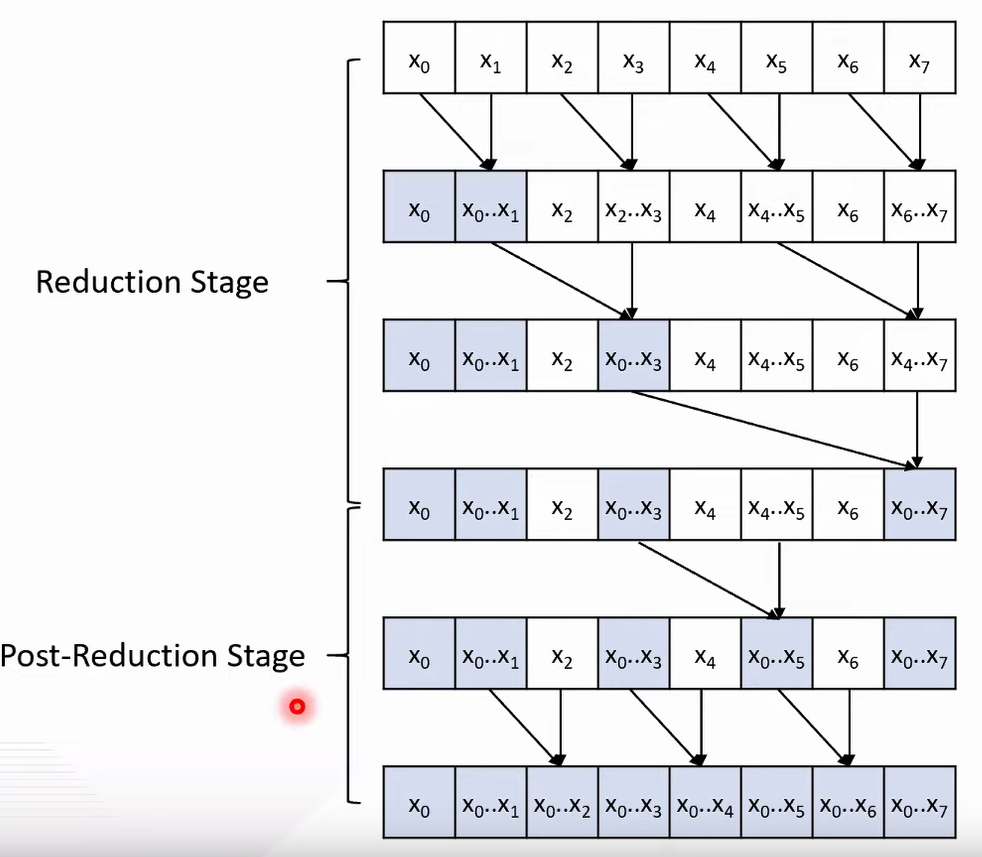
Brent-Kung
- Brent-Kung takes more steps but is more work-efficient
Brent-Kung example with 8 elements
Analysis
- Reduction stage:
- log(N) steps
- N/2+N/4+…+2+1=N−1 operations
- Post-reduction stage:
- log(N)−1 steps
- (2−1)+(4−1)+…+(N/2−1)=(N−2)−(log(N)−1) operations
- Total:
- 2∗log(N)−1 steps
- 2∗N−log(N)−2=O(N) operations